Stack Organization

A stack, also known as a last-in, first-out (LIFO) list, is a crucial feature in the CPU of most computers. It stores information in a manner where the last item stored is the first to be retrieved. This can be compared to a stack of trays: the last tray placed on top is the first one to be removed.

In digital computers, a stack is essentially a memory unit with an address register that only counts (after an initial value is loaded). This register, known as the stack pointer (SP), always points to the top item in the stack. Unlike a physical stack of trays where items are physically removed or added, the stack in a computer retains all physical registers for reading or writing; it's the content of these words that is manipulated.

Stack Operations

The two fundamental operations of a stack are:

1. Push: The operation of inserting an item into the stack.
2. Pop: The operation of removing an item from the stack.

When pushing an item, the stack pointer is incremented, and the item is written to the new top position. When popping an item, the item is read from the current top position, and the stack pointer is decremented.

Register Stack

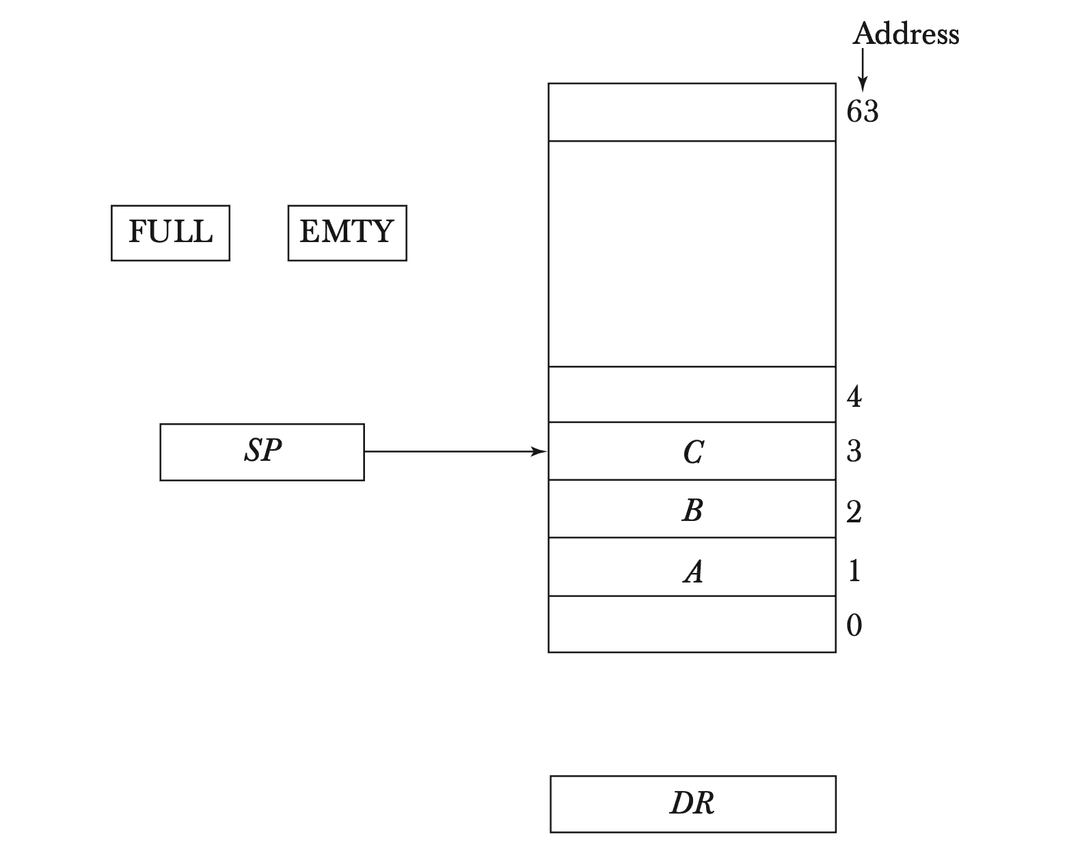
A stack can be implemented as a section of a larger memory or as a collection of finite memory words or registers. Consider a 64-word register stack:

• The stack pointer (SP) holds the address of the top word in the stack.
• When items are pushed or popped, SP is incremented or decremented accordingly.
• SP is a 6-bit register because $2^6 = 64$. Therefore, SP can address from 0 to 63.

Example

If three items A, B, and C are pushed into the stack in that order:

• SP initially points to address 0.
• After pushing A, SP is incremented to 1.
• After pushing B, SP is incremented to 2.
• After pushing C, SP is incremented to 3.

To pop an item, the stack is read from the current SP address, and SP is decremented. For instance, popping C (at SP=3) decrements SP to 2, making B the new top item.

Stack Overflow and Underflow

• Overflow: Occurs when trying to push an item into a full stack.
• Underflow: Occurs when trying to pop an item from an empty stack.

To manage these conditions:

• A 1-bit FULL register indicates if the stack is full.
• A 1-bit EMTY register indicates if the stack is empty.

Microoperations

Push Operation

1. Increment SP.
2. Write item to the stack.

SP <- SP + 1
M[SP] <- DR

3. Check if stack is full and set FULL flag if true.
4. Clear EMTY flag.

Pop Operation

1. Read item from the stack.
2. Decrement SP.

DR <- M[SP]
SP <- SP - 1
M[SP] <- DR

3. Check if stack is empty and set EMTY flag if true.
4. Clear FULL flag.

Memory Stack

Stacks can also be implemented using a section of random-access memory (RAM) rather than dedicated registers. In this case, the stack pointer still manages stack operations, but it points to memory addresses within the assigned stack section.

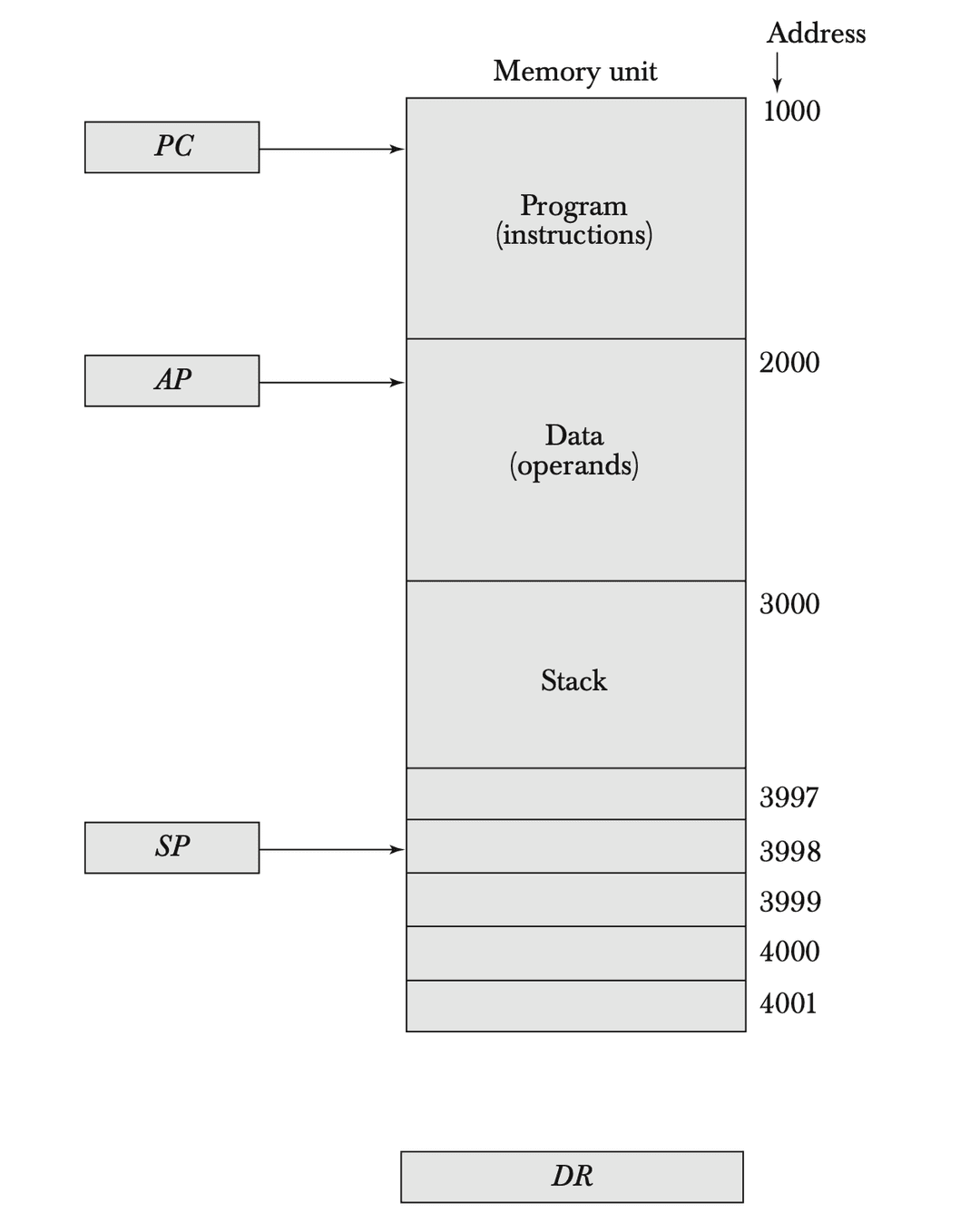
Example

In a memory stack with initial SP value 40, and the stack growing downward:

• First item is stored at address 40.
• Second item at address 39.
• SP is decremented for each push and incremented for each pop.

Arithmetic Expressions and Reverse Polish Notation (RPN)

Arithmetic expressions can be written in various notations: infix, prefix (Polish), and postfix (Reverse Polish). Each notation has its use cases and benefits, particularly in how they are processed by computers and calculators.

Notations

1. Infix Notation:

   • The operator is placed between the operands (e.g., $A + B$).
   • Commonly used in everyday arithmetic and most programming languages.
   • Requires parentheses to indicate the order of operations (e.g., $(A + B) \cdot (C + D)$).
   • Hierarchy and precedence rules must be respected (e.g., multiplication before addition).

2. Prefix Notation (Polish Notation):

   • The operator precedes the operands (e.g., $+ A B$).
   • Eliminates the need for parentheses since the order of operations is inherently unambiguous.
   • Less intuitive for humans but straightforward for computers to parse.

3. Postfix Notation (Reverse Polish Notation, RPN):

   • The operator follows the operands (e.g., $A B +$).
   • Also eliminates the need for parentheses and respects the natural order of operations.
   • Highly efficient for stack-based evaluation, making it well-suited for computer algorithms and certain calculators.

Conversion Between Notations

Infix to Postfix Conversion

To convert an infix expression to postfix, the following algorithm can be used:

1. Initialize an empty stack for operators and an empty list for the output.
2. Read the infix expression from left to right.
3. Process each token:
   • If the token is an operand, append it to the output list.
   • If the token is an operator, pop from the stack to the output list until the stack is empty or the top of the stack has an operator of lower precedence. Push the current operator onto the stack.
   • If the token is a left parenthesis, push it onto the stack.
   • If the token is a right parenthesis, pop from the stack to the output list until a left parenthesis is encountered. Remove the left parenthesis from the stack.
4. Pop any remaining operators from the stack to the output list.

Example

Convert the infix expression $(A + B) \cdot (C - D)$ to postfix:

1. Initialize an empty stack and output list.
2. Read and process each token:
   • $($: Push to stack.
   • $A$: Append to output.
   • $+$: Push to stack.
   • $B$: Append to output.
   • $)$: Pop and append to output until $($: Output: A B +.
   • $\cdot$: Push to stack.
   • $($: Push to stack.
   • $C$: Append to output.
   • $-$: Push to stack.
   • $D$: Append to output.
   • $)$: Pop and append to output until $($: Output: A B + C D -.
3. Pop remaining operators: Output: A B + C D - \cdot.

The postfix expression is $A B + C D - \cdot$.

Evaluation of Postfix Expressions

The evaluation of postfix expressions using a stack is straightforward:

1. Initialize an empty stack.
2. Read the postfix expression from left to right.
3. Process each token:
   • If the token is an operand, push it onto the stack.
   • If the token is an operator, pop the required number of operands from the stack, perform the operation, and push the result back onto the stack.
4. The final result will be the only item remaining on the stack.

Example

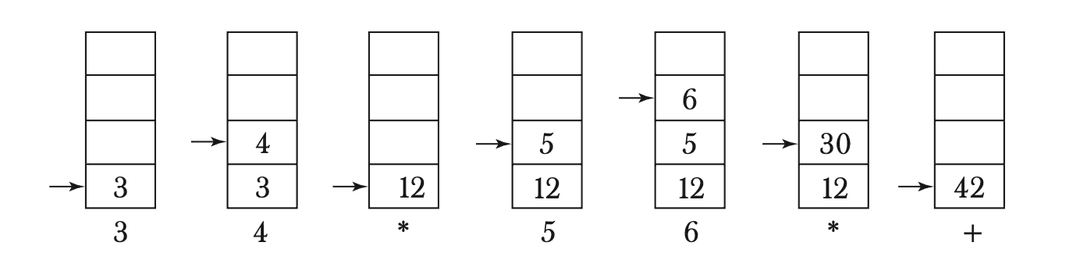
Evaluate the postfix expression $3 4 \cdot 5 6 \cdot +$:

1. Initialize an empty stack.
2. Read and process each token:
   • $3$: Push onto stack.
   • $4$: Push onto stack.
   • $\cdot$: Pop 4 and 3, compute $3 \cdot 4 = 12$, push 12.
   • $5$: Push onto stack.
   • $6$: Push onto stack.
   • $\cdot$: Pop 6 and 5, compute $5 \cdot 6 = 30$, push 30.
   • $+$: Pop 30 and 12, compute $12 + 30 = 42$, push 42.
3. The final result is 42.

Advantages of RPN and Stacks

1. Simplicity: RPN removes the need for parentheses, simplifying the expression.
2. Efficiency: Stack-based evaluation reduces the need for temporary storage and intermediate variable handling.
3. Direct Mapping to Machine Instructions: Many CPU architectures support stack operations directly, making RPN an efficient choice for expression evaluation in low-level programming.

A stack-organized CPU can efficiently handle arithmetic expressions and complex calculations using a straightforward set of operations. This method is widely used in both calculators and computer systems, demonstrating its versatility and effectiveness in processing sequential data. The consistent use of a stack pointer ensures that the CPU can access and update stack addresses automatically, enhancing computational efficiency.

By converting expressions to Reverse Polish Notation and utilizing a stack-based evaluation method, the computational process becomes more streamlined, with a clear order of operations and reduced need for intermediate storage. This not only simplifies the implementation of arithmetic operations but also leverages the inherent advantages of stack architecture in processing complex and nested calculations.