Representation of Floating-Point Numbers
Floating-point representation is a method used to encode real numbers within the limits of finite precision available in computer systems. This representation divides a number into two main parts: the mantissa and the exponent.
Components of Floating-Point Representation
- Mantissa: The mantissa represents a signed, fixed-point number. It can be a fraction or an integer.
- Exponent: The exponent determines the position of the radix point (decimal or binary point).
Example in Decimal
Consider the decimal number +6132.789. In floating-point representation, it can be split into:
- Fraction: +0.6132789
- Exponent: +04
This indicates that the actual decimal point is four positions to the right of the implied decimal point in the fraction. The complete representation in scientific notation is:
General Form
Floating-point numbers are generally represented in the form:
Where:
- is the mantissa.
- is the exponent.
- is the radix (base of the number system, e.g., 10 for decimal, 2 for binary).
Only the mantissa and the exponent are stored in the register, along with their respective signs. The radix and the assumed position of the radix point are implicitly understood by the processing circuits.
Binary Floating-Point Representation
In binary systems, the floating-point representation follows a similar structure but uses base 2. For example, the binary number +1001.11 can be represented as follows:
- Fraction: 01001110 (with an implied binary point after the sign bit)
- Exponent: 000100
The equivalent representation is:
Normalization
A floating-point number is considered normalized if the most significant digit of the mantissa is nonzero. For instance:
- Normalized: 350 (in decimal) or 11010000 (in 8-bit binary after normalization).
- Non-normalized: 00035 (in decimal) or 00011010 (in 8-bit binary).
To normalize a binary number like 00011010, you would shift the digits three positions to the left, yielding 11010000, and adjust the exponent accordingly by subtracting 3.
Normalized numbers maximize the precision of floating-point representation. A zero cannot be normalized and is usually represented by all zeros in both the mantissa and the exponent.
Floating-Point Arithmetic
Arithmetic operations with floating-point numbers are more complex than those with fixed-point numbers. This complexity arises from the need to align exponents before performing operations and to normalize results after operations. Despite the complexity, floating-point arithmetic is essential for scientific computations due to the vast range of values it can represent. Modern computers and calculators typically have built-in hardware for floating-point arithmetic. For systems without such hardware, software routines are provided to handle these operations.
Other Binary Codes
Gray Code
The Gray code, or reflected binary code, is used in various digital systems for minimizing errors during transitions between values. Each subsequent value in Gray code differs from the previous one by only a single bit. This property is particularly useful in analog-to-digital conversion processes, where it reduces ambiguity during state transitions.
Example of Gray Code
A 4-bit Gray code sequence might look like this:
- 0000 (0)
- 0001 (1)
- 0011 (2)
- 0010 (3)
- 0110 (4)
- 0111 (5)
- 0101 (6)
- 0100 (7)
- 1100 (8)
- 1101 (9)
- 1111 (10)
- 1110 (11)
- 1010 (12)
- 1011 (13)
- 1001 (14)
- 1000 (15)
Gray code is often utilized in systems where error minimization is critical, such as in rotary encoders and digital counters.
Other Decimal Codes
Digital systems also use various binary codes to represent decimal digits, each with its specific applications and properties. Some common binary codes for decimal digits include:
- BCD (Binary-Coded Decimal): Directly represents each decimal digit with its binary equivalent.
- 2421 Code: A weighted code where each bit is weighted by 2, 4, 2, and 1 respectively.
- Excess-3 Code: Derived from BCD by adding 3 (0011) to each binary-coded digit.
- Excess-3 Gray Code: A variation of Gray code adapted for decimal digits.
Example of BCD and Excess-3 Codes
-
BCD:
- 0: 0000
- 1: 0001
- 2: 0010
- 3: 0011
- 4: 0100
- 5: 0101
- 6: 0110
- 7: 0111
- 8: 1000
- 9: 1001
-
Excess-3:
- 0: 0011
- 1: 0100
- 2: 0101
- 3: 0110
- 4: 0111
- 5: 1000
- 6: 1001
- 7: 1010
- 8: 1011
- 9: 1100
Self-Complementing Codes
Some codes, like the 2421 and Excess-3, are self-complementing, meaning the 9's complement of a number is easily obtained by inverting all bits. This property is advantageous for certain arithmetic operations, particularly when using signed-complement representations.
Alphanumeric Codes
ASCII
The ASCII (American Standard Code for Information Interchange) is a 7-bit code used to represent text in computers and communication devices. It includes control characters, numerals, uppercase and lowercase letters, and various symbols.
EBCDIC
EBCDIC (Extended Binary Coded Decimal Interchange Code) is another alphanumeric code used mainly in IBM systems. It uses 8 bits per character, allowing for a larger set of symbols compared to ASCII.
6-Bit Codes
For internal processing, some systems use 6-bit codes to represent a reduced set of characters, typically including uppercase letters, digits, and a limited set of special characters. This reduces memory usage, making it suitable for certain data processing applications.
By understanding these various binary and alphanumeric codes, one can better appreciate the methods used for representing and manipulating data in digital systems.
Error Detection Codes
Binary information transmitted through communication channels is prone to errors due to external noise, which may flip bits from 1 to 0 or vice versa. An error detection code is a binary code that identifies errors during transmission. Although these codes cannot correct the detected errors, they can signal their presence, prompting retransmission or system checks.
Parity Bit
The most common error detection code is the parity bit. A parity bit is an additional bit included with a binary message to ensure that the total number of 1s is either odd or even. The procedure for generating parity bits can be summarized as follows:
Types of Parity
- Odd Parity: The parity bit is chosen so that the total number of 1s, including the parity bit, is odd.
- Even Parity: The parity bit is chosen so that the total number of 1s, including the parity bit, is even.
For a message consisting of three bits, the possible parity bits are shown below:
| Message (xyz) | P(odd) | P(even) |
|---|---|---|
| 000 | 1 | 0 |
| 001 | 0 | 1 |
| 010 | 0 | 1 |
| 011 | 1 | 0 |
| 100 | 0 | 1 |
| 101 | 1 | 0 |
| 110 | 1 | 0 |
| 111 | 0 | 1 |
Parity Bit Generation and Checking
During data transmission, the parity bit is used as follows:
- Sending End: The message is input to a parity generator, which computes the required parity bit.
- Transmission: The message, including the parity bit, is sent to the receiver.
- Receiving End: The received bits are input to a parity checker, which verifies the parity. An error is detected if the parity does not match the expected value.
Parity Bit Example
Consider a 3-bit message transmitted with an odd parity bit. At the sender, an odd-parity bit is generated, and the message is sent. Upon reception, the parity checker examines the parity:
- If the total number of 1s is even, an error is detected (since the original message had odd parity).
Parity Bit Logic
Parity generation and checking utilize exclusive-OR (XOR) and exclusive-NOR (XNOR) logic gates. The XOR function for three or more variables is an odd function, which is true if and only if an odd number of inputs are 1.
For even parity, the XOR of the message bits is computed:
For odd parity, the XNOR gate complements the XOR result:
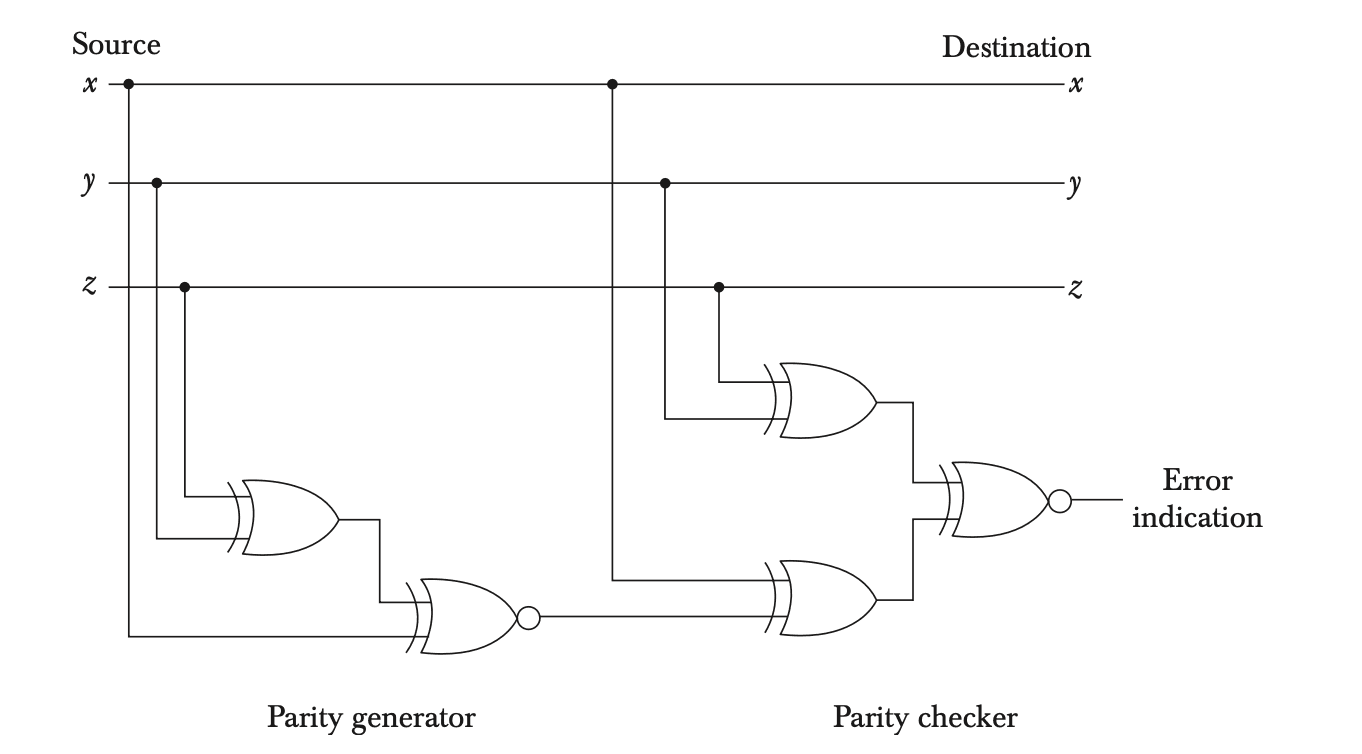
Parity Bit Circuit
A typical parity generator and checker circuit is illustrated below. The generator uses one XOR gate and one XNOR gate for odd parity:
- Parity Generator: Computes the parity bit at the sender's end.
- Parity Checker: Verifies the parity at the receiver's end.
The generator circuit for odd parity consists of an XOR gate followed by an XNOR gate to ensure the parity bit results in an odd number of 1s.
Error Detection with Parity
The parity method detects the presence of one, three, or any odd number of errors. However, it cannot detect an even number of errors. Despite this limitation, parity bits are a simple and effective means of error detection in many practical applications.
Example Parity Generation and Checking
Consider a message to be transmitted with odd parity. At the sender:
- Compute .
- Transmit .
At the receiver:
- Check parity using .
- An error is detected if the parity of the received bits is even.
This circuit can also be adapted for even parity by using only XOR gates, as even parity does not require complementation.
Unified Parity Circuit
A unified circuit can be used for both parity generation and checking by permanently setting one input to logic-0 during parity generation. This allows the same hardware to serve dual functions, optimizing resource usage.
In summary, parity bits are a fundamental tool in error detection, offering a balance between simplicity and effectiveness. Despite their inability to correct errors or detect even-numbered errors, they remain widely used due to their low overhead and ease of implementation.